5.2 正六角形

5.2.1 円に内接する正六角形を描く

（1）円Oの円周上の任意の点Aを中心として円Oと同一半径の弧を描き、交点をB,Fとする。

（2）Bより同一半径の弧を描いて交点Cを求め、同様にして順次交点D,Eを求める。A,B,C,D,E,F,Aを順次直線で結べば正六角形となる。

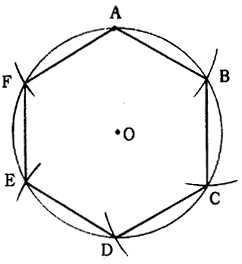
図1.22

5.2.2 一辺が与えられた正六角形を描く

（1）与えられた一辺ABのA,B点各々を中心として半径ABの弧を描き、その交点をOとする。

（2）Oを中心として半径ABの円を描き、その円周を半径ABで分割した点をC,D,E,Fとすれば、B,C,D,E,F,Aを結ぶ図形は正六角形となる。

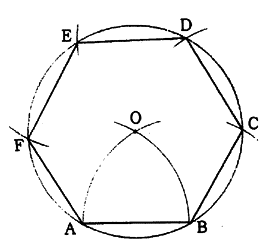
図1.23

5.3 任意の正多角形

5.3.1 円に内接する任意の正多角形を描く

4.1.3で述べた「円周を任意の数に等分する」方法と同様である。円周の等分点を順次直線で結べば、求める正多角形が得られる。

5.3.2 一辺が与えられた任意の正多角形を描く

（1）与えられた一辺ABのAを中心として半径ABの弧を描き、ABの延長線上の交点をCとする。

（2）B,C各々を中心とする半径BCの弧を描き、両弧の交点をDとする。

（3）CBを求める正多角形の辺数に等分する。ここでは例えば7等分するとする。

（4）Dと第2等分点2とを結び、その延長線と弧BCとの交点をEとすれば、AEは求める多角形の第2辺となる。

（5）ABとAEの垂直2等分線の交点をOとしてAOを半径とする円を描き、その円周をABで等分割すれば、求める正多角形が得られる。

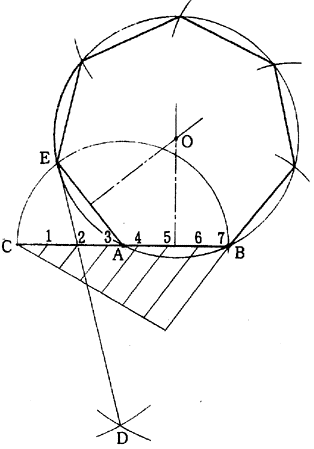
図1.24

前ページ　　　目次へ　　　次ページ